最短路徑優(yōu)先算法�����,正如OSPF路由協(xié)議的名字所告訴我們的�,該協(xié)議用來(lái)計(jì)算路由的算法,稱為最短路徑優(yōu)先(Shortest Path First)算法�。該算法是由一位荷蘭計(jì)算機(jī)科學(xué)家Dijkstra于1959年發(fā)現(xiàn)的,所以該算法又稱為Dijkstra算法���。
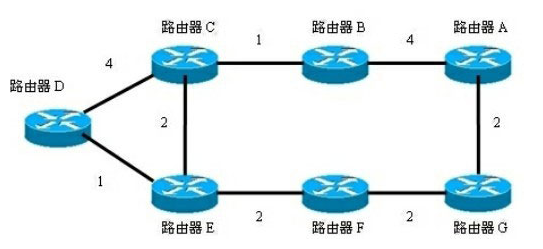
該算法把網(wǎng)絡(luò)考慮為一組點(diǎn)到點(diǎn)連接的結(jié)點(diǎn)���,每條鏈路有一個(gè)開(kāi)銷值,每個(gè)結(jié)點(diǎn)有它自己的名字及一個(gè)包含已知物理拓?fù)涞耐暾溌沸畔⒌臄?shù)據(jù)庫(kù)��。圖1 表現(xiàn)了一個(gè)這樣的網(wǎng)絡(luò)����。
圖1 運(yùn)行OSPF的網(wǎng)絡(luò)環(huán)境
表1描述了圖1中每一臺(tái)路由器到達(dá)鄰居路由器的鏈路開(kāi)銷�。
表1 在圖1中各個(gè)路由器到達(dá)鄰居路由器的鏈路開(kāi)銷

在圖1及表1中��,我們可以看到整個(gè)網(wǎng)絡(luò)的拓?fù)?����,這就是反映在路由器的拓?fù)浔砝锏木W(wǎng)絡(luò)信息�����。
但是���,這個(gè)拓?fù)溥€有環(huán)路存在����。比如��,從路由器B到達(dá)路由器D就存在著環(huán)路��,數(shù)據(jù)包經(jīng)過(guò)路由器A和路由器C都可以到達(dá)路由器D�����。我們需要使用最短路徑優(yōu)先算法從這個(gè)拓?fù)渲杏?jì)算出最短路徑優(yōu)先樹(shù)�。在計(jì)算出路由的同時(shí),避免路由環(huán)路��。
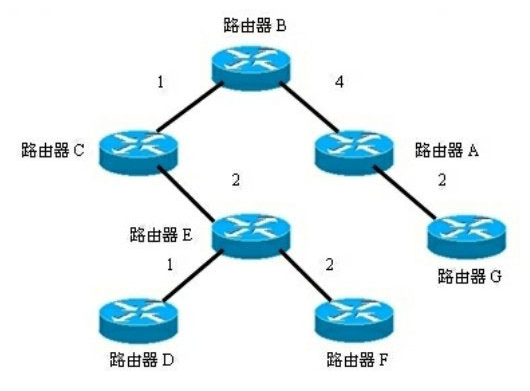
圖2顯示了在路由器B上經(jīng)過(guò)最短路徑優(yōu)先算法計(jì)算之后形成的樹(shù)型結(jié)構(gòu)��。
圖2 在路由器B上經(jīng)過(guò)最短路徑優(yōu)先算法計(jì)算之后形成的樹(shù)型結(jié)構(gòu)
從圖2我們可以看出��,從路由器B到路由器D的最短路徑���,并不是經(jīng)過(guò)路由器C直接到達(dá)路由器D�����,因?yàn)檫@條路徑的開(kāi)銷比經(jīng)過(guò)路由器C和路由器E這條路徑的開(kāi)銷還要大�����。在最短路徑優(yōu)先算法中���,到達(dá)目的網(wǎng)段開(kāi)銷最低的那條路徑是最短的路徑。
圖2實(shí)際上就是路由器B的路由表的圖形化表現(xiàn)形式��。